二分查找又称折半查找,厂房保洁13825404095优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
Bentley在他的著作《Writing Correct Programs》中写道,90%的计算机专家不能在2小时内写出完全正确的二分搜索算法。问题的关键在于准确地制定各次查找范围的边界以及终止条件的确定,正确地归纳奇偶数的各种情况,其实整理后可以发现它的具体算法是很直观的。
折半查找法的优点是比较次数少,查找速度快,平均性能好; 其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。
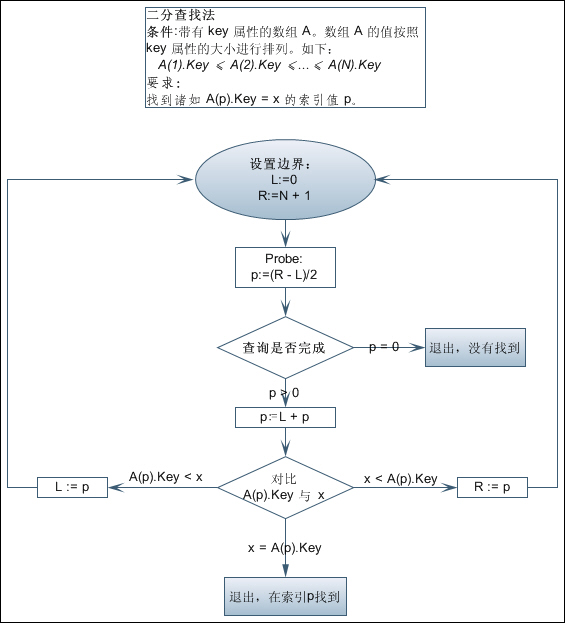
算法步骤描述
① 首先确定整个查找区间的中间位置 mid = ( left + right )/ 2
② 用待查关键字值与中间位置的关键字值进行比较;
若相等,则查找成功
若大于,则在后(右)半个区域继续进行折半查找
若小于,则在前(左)半个区域继续进行折半查找
③ 对确定的缩小区域再按折半公式,重复上述步骤。
最后,得到结果:要么查找成功, 要么查找失败。折半查找的存储结构采用一维数组存放。
折半查找算法举例
对给定数列(有序){ 3,5,11,17,21,23,28,30,32,50,64,78,81,95,101},按折半查找算法,查找关键字值为81的数据元素。
折半查找的算法讨论:
优点:ASL≤log2n,即每经过一次比较,查找范围就缩小一半。经log2n 次计较就可以完成查找过程。
缺点:因要求有序,所以要求查找数列必须有序,而对所有数据元素按大小排序是非常费时的操作。另外,顺序存储结构的插入、删除操作不便利。
考虑:能否通过一次比较抛弃更多的部分(即经过一次比较,使查找范围缩得更小),以达到提高效率的目的。……?
可以考虑把两种方法(顺序查找和折半查找)结合起来,即取顺序查找简单和折半查找高效之所长,来达到提高效率的目的?实际上这就是分块查找的算法思想。
Java二分查找源码
package com.thread.wait.test;
public class BinarySearch {
/**
* 二分查找算法 : 在有序表R[0..n-1]中进行二分查找,成功时返回结点的位置,失败时返回-1
*
* @param srcArray
*
有序数组
* @param key
*
查找元素
* @return key的数组下标,没找到返回-1
* */
public static void main(String[] args) {
int srcArray[] = { 3, 5, 11, 17, 21, 23, 28, 30, 32, 50, 64, 78, 81,
95, 101 };
System.out.println(binSearch(srcArray, 0, srcArray.length - 1, 81));
}
/**
* 二分查找递归实现
*
* @param srcArray
* @param start
* @param end
* @param key
* @return
*/
public static int binSearch(int srcArray[], int start, int end, int key) {
int mid = (end - start) / 2 + start;
if (srcArray[mid] == key) {
return mid;
}
if (start >= end) {
return -1;
} else if (key > srcArray[mid]) {
return binSearch(srcArray, mid + 1, end, key);
} else if (key < srcArray[mid]) {
return binSearch(srcArray, start, mid - 1, key);
}
return -1;
}
/**
* 二分查找普通循环实现
*
* @param srcArray
* @param key
* @return
*/
public static int binSearch(int srcArray[], int key) {
int mid = srcArray.length / 2;
if (key == srcArray[mid]) {
return mid;
}
int start = 0;
int end = srcArray.length - 1;
while (start <= end) {
// 使用 (low + high) / 2 会有整数溢出的问题
mid = (end - start) / 2 + start;
if (key < srcArray[mid]) {
// 继续在R[low..mid-1]中查找
end = mid - 1;
} else if (key > srcArray[mid]) {
// 继续在R[mid+1..high]中查找
start = mid + 1;
} else {
return mid;
}
}
// 当low>high时表示查找区间为空,查找失败
return -1;
}
}
